Алгоритм Дейкстры
Данный алгоритм был разработан нидерландским ученым Эдгсгером Дейкстрой, из-за чего получил такое название. Алгоритм Дейкстры находит кратчайшие пути из заданной вершины до всех остальных. С помощью данного алгоритма на практике мы можем узнать, как быстрее добраться из города A в город B по дороге. Это значит, что данный алгоритм имеет достаточно большую распространенность, в том числе и в GPS - навигации.
Однако у этого алгоритма есть существенный минус. Этот минус заключается в том, что алгоритм Дейкстры не умеет работать с ребрами отрицательного веса. Поясним на примере: допустим, что существует такая дорога. И проезд по ней будет убыточным для вашей фирмы. В решении данного вопроса алгоритм Дейкстры нам не поможет. Но, не стоит расстраиваться, ведь существуют другие алгоритмы поиска кратчайшего пути, и в них данный недостаток до настоящего времени не наблюдался (см. Алгоритм Фллойда - Уоршелла).
Принцип
Рассмотрим следующий взвешенный орграф:
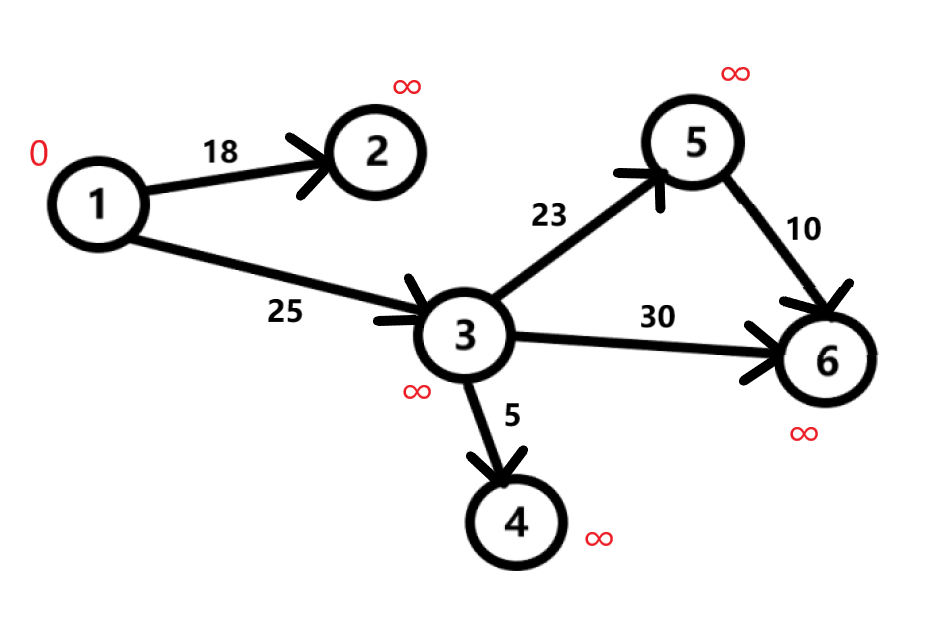
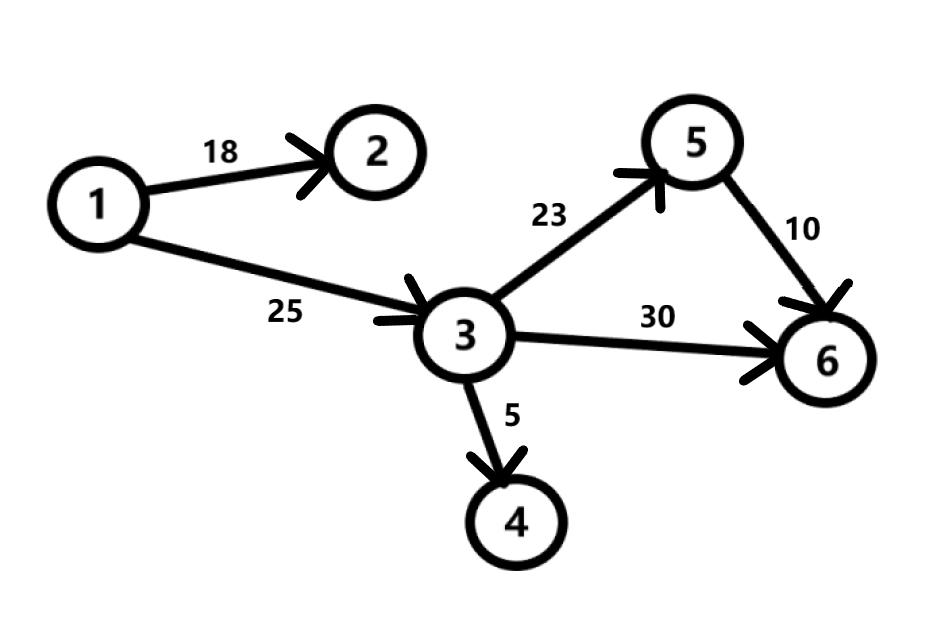 Присвоим всем вершинам кроме данной расстояние бесконечность, а данной вершине 0 (т.к между одной и той же вершиной расстояние равно 0).
Присвоим всем вершинам кроме данной расстояние бесконечность, а данной вершине 0 (т.к между одной и той же вершиной расстояние равно 0).
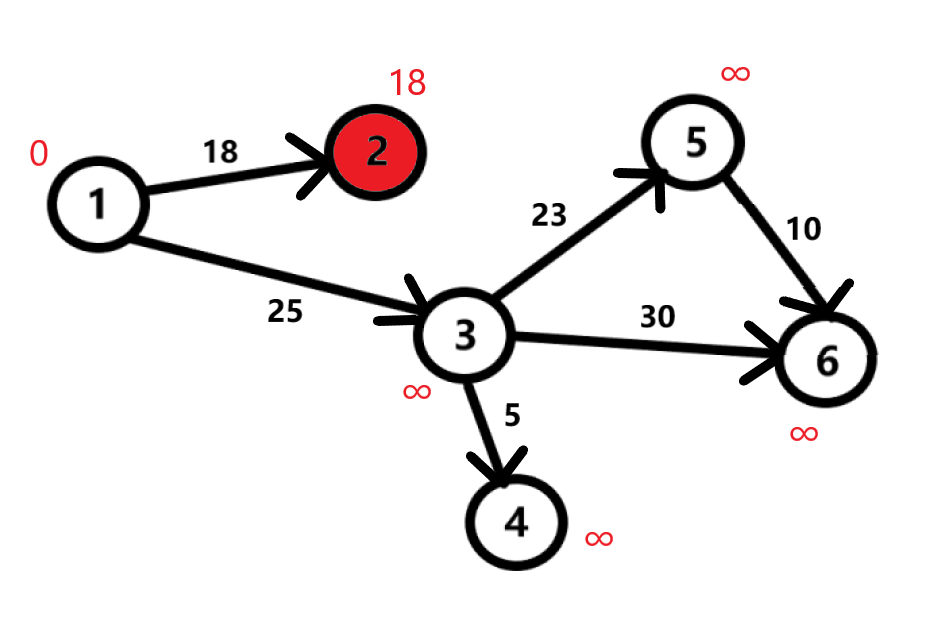
 Идем к вершине 2. Смотрим: расстояние предыдущей вершины 1 равно 0, а расстояние до 2 равно 18. Производим несложное сравнение: \(0 + 18 \lt \infty\). Присваиваем расстоянию до 2 18. Из этой вершины нет путей в другие вершины, поэтому отмечаем 2 как посещенную.
Идем к вершине 2. Смотрим: расстояние предыдущей вершины 1 равно 0, а расстояние до 2 равно 18. Производим несложное сравнение: \(0 + 18 \lt \infty\). Присваиваем расстоянию до 2 18. Из этой вершины нет путей в другие вершины, поэтому отмечаем 2 как посещенную.
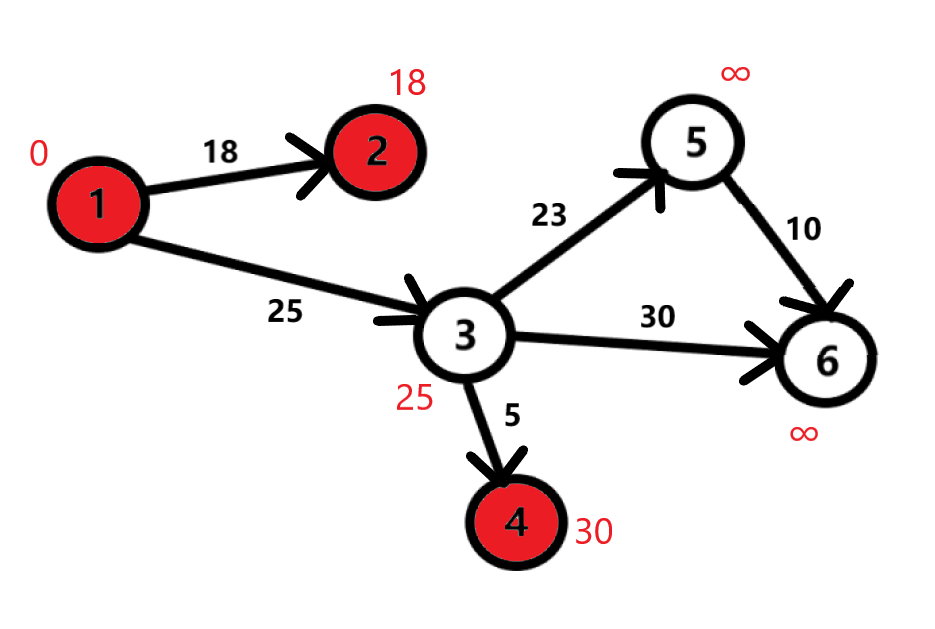
 Аналогичные действия проделываем с 3 и 4 вершинами.
Аналогичные действия проделываем с 3 и 4 вершинами.
 Переходим к вершине 5. Присваиваем расстоянию до неё \(48\). Далее рассматриваем вершину 6. Присваиваем расстоянию \(55\). Больше нет ребер из вершины 3, значит отмечаем её как посещенную. Переходим к рассмотрению вершины 5.
Переходим к вершине 5. Присваиваем расстоянию до неё \(48\). Далее рассматриваем вершину 6. Присваиваем расстоянию \(55\). Больше нет ребер из вершины 3, значит отмечаем её как посещенную. Переходим к рассмотрению вершины 5.
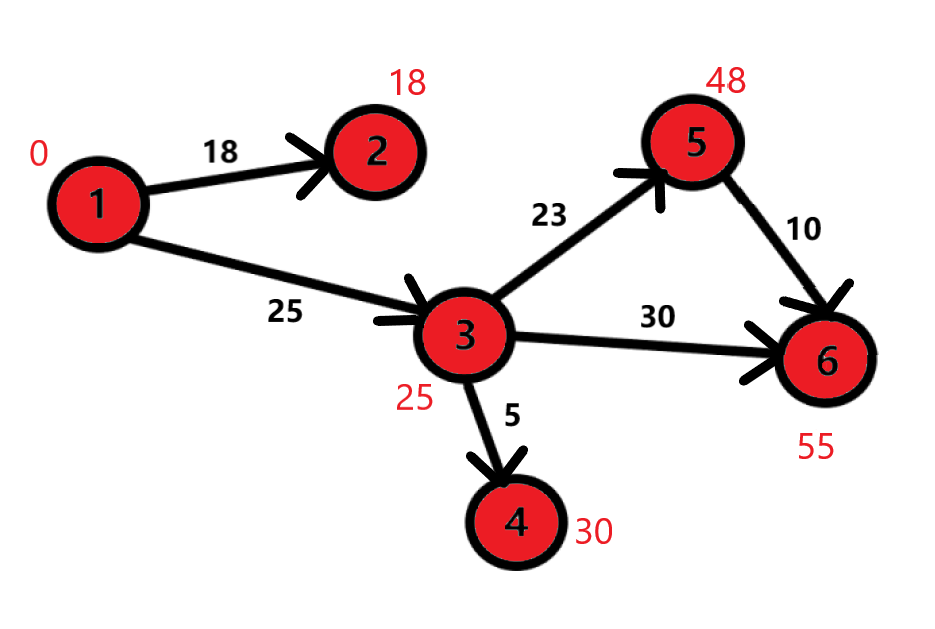
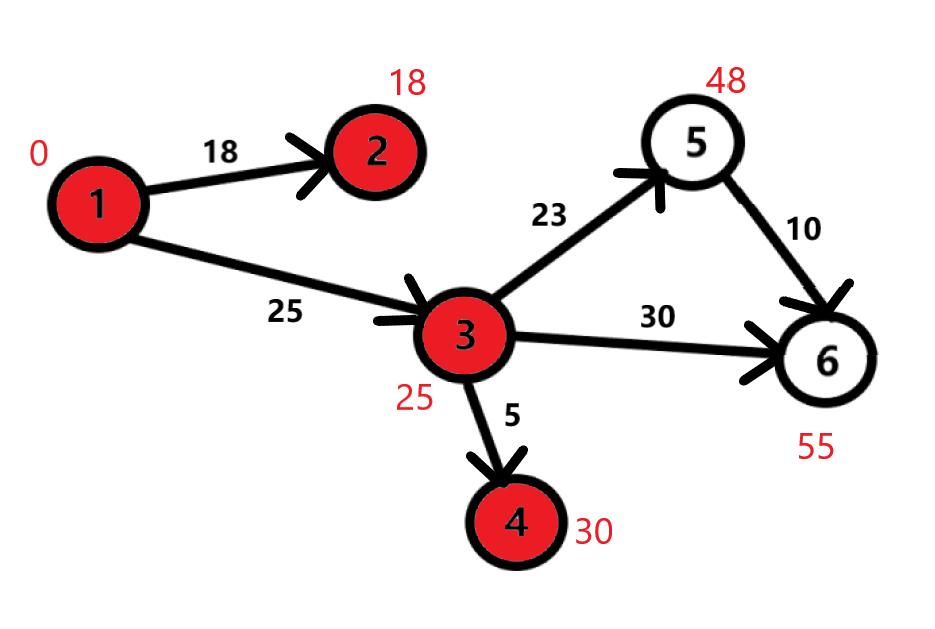 Здесь, как можно заметить, мы можем присвоить расстояние до 6 вершины \(58\). Но у нас уже имеется меньшее число - \(55\). В таком случае оставляем как есть. Отмечаем вершины 6 и 5 как посещенные. Алгоритм завершает свою работу. Таким образом, мы нашли короткие расстояния из первой вершины до всех остальных.
Здесь, как можно заметить, мы можем присвоить расстояние до 6 вершины \(58\). Но у нас уже имеется меньшее число - \(55\). В таком случае оставляем как есть. Отмечаем вершины 6 и 5 как посещенные. Алгоритм завершает свою работу. Таким образом, мы нашли короткие расстояния из первой вершины до всех остальных.
Реализация
Для реализации алгоритма Дейкстры нам потребуется два массива: один, логический, visited, для того, чтобы отмечать посещенные вершины; также нам потребуется численный distance, для хранения найденных кратчайших путей. Изначально все элементы массива visited обозначены как false. В каждый элемент массива distance мы запишем такое число, которое больше любого потенциально короткого пути. Для удобства будем называть такое число бесконечностью. Однако, это числе не является бесконечностью в прямом смысле этого слова, просто это очень большое число. В данном случае мы будем использовать INT_MAX. В качестве вершины, с которой мы начнем обход, будем использовать вершину a. Поэтому, distance[a] = 0 (алгоритм не предусматривает петель).
Алгоритм
const int v = 6; // число вершин
void Dijkstra(int graph[v][v], int start)
{
int distance[v],index;
bool visited[v];
for (int i = 0; i < v; i++)
{
distance[i] = INT_MAX;
visited[i] = false;
}
distance[start] = 0;
for (int i = 0; i < v-1; i++)
{
int min = INT_MAX;
for(int j = 0;j < v;j++)
if (!visited[j] && distance[j] < min)
{
min = distance[j];
index = j;
}
visited[index] = true;
for(int j = 0; j < v; j++)
if (!visited[j] && graph[index][j] && distance[index] != INT_MAX &&
distance[index] + graph[index][j] < distance[j])
distance[j] = distance[index] + graph[index][j];
}
for (int i = 0; i < v; i++)
if (distance[i] != INT_MAX)
cout << start + 1 << " > " << i+1 << " = " << distance[i] << endl;
else
cout << start + 1 << " > " << i+1 << " = " << "not available" << endl;
}int main() {
int graph[v][v] = {
{0, 18, 25, 0, 0, 0},
{18, 0, 0, 0, 0, 0},
{25, 0, 0, 5, 23, 30},
{0, 0, 5, 0, 0, 0},
{0, 0, 23, 0, 0, 10},
{0, 0, 30, 0, 10, 0},
};
int start;
cout << "Enter the start vertex: ";
cin >> start;
Dijkstra(graph, start-1);
return 0;
}
Массив graph это модифицированная матрица смежности. \(0\) означает отсутствие вершины, а числа показывают расстояния от вершины \(i\) до вершины \(j\).