Поиск компоненты связности
Компонента связности - набор вершин графа, в котором между любой парой вершин существует путь. В свою очередь одна вершина тоже составляет компоненту связности.
На данном изображении три компоненты связности
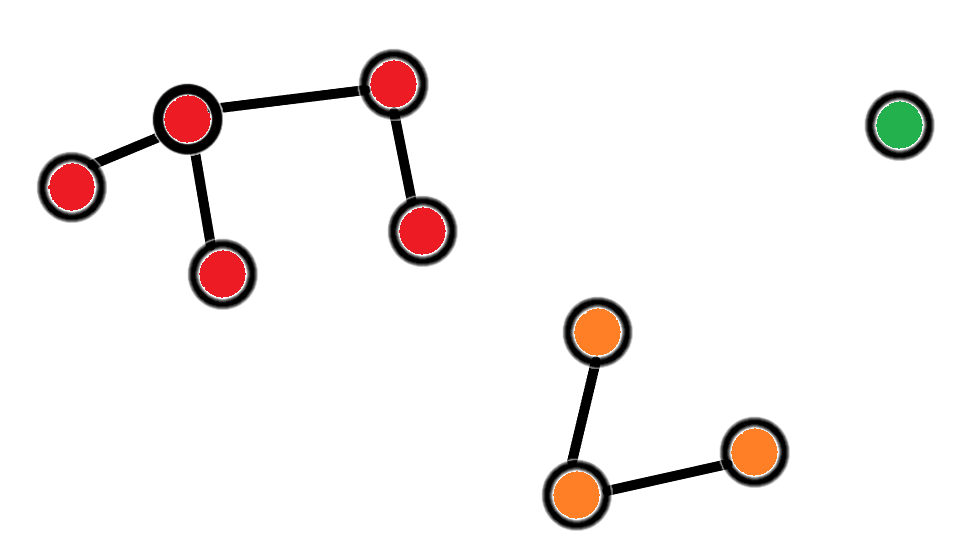
Определение, данное нами выше, распространяется на неориентированные графы. Для ориентированных графов применяют такие понятия как слабая и сильная связность. В данной статье данные эти понятия рассматриваться не будут.
Алгоритм
Как найти компоненты связности?
Для этого нам нужно использовать один из двух методов обхода графа (BFS / DFS). При запуске обхода из одной вершины, он гарантированно посетит все вершины, до которых возможно добраться, то есть, всю компоненту связности, к которой принадлежит начальная вершина. Для нахождения всех компонент просто попытаемся запустить обход из каждой вершины по очереди, если мы ещё не обошли её компоненту ранее.
Каждую компоненту связности будем нумеровать, для чего создадим массив компонент \(comp\).
bool used[100];
vector <vector<int>> graph(100);
int comp[100];
void dfs(int vertex, int components)
{
used[vertex] = true;
comp[vertex] = components;
for (auto u : graph[vertex])
{
if (!used[u])
dfs(u, components);
}
}
int main()
{
int n,m;
int components = 1; // нумеруем компоненты с 1
cout << "Enter the number of edges: ";
cin >> n;
cout << "Enter the number of vertexes: ";
cin >> m;
for (int i = 0; i < n; i++)
{
int a, b;
cin >> a >> b;
graph[a].push_back(b);
graph[b].push_back(a);
}
for (int i = 1; i <= m; i++) {
if (!used[i]) { //если мы ещё не посетили эту вершину, обходя одну из предыдущих
dfs(i, components);
components++;
}
}
for (int i = 1; i <= m; i++) {
cout << "Vertex " << i << " belongs to component #" << comp[i] << endl;
}
return 0;
}Таким образом, мы можем узнать, что такая вершина принадлежит такой-то компоненте связности.